An Introduction to Shaders in openGL

An Introduction to Shaders in openGL

Recently I became interested in graphics programming, specifically shaders. Alot of tutorials are very high level and don’t try to teach you what’s happening under the hood. I wanted to understand things happening under the hood. Below is my annotation for a set of openGL tutorials.

1 — Choose your language, platform.

I chose openGL, specifically PyOpenGL. openGL is an open standard maintained by many companies through Khronos. It’s very flexible and runs on basically every system. Other choices would be DirectX 12 (the closed source microsoft windows graphics library) and Vulkan a more powerful but lower level successor to openGL (open source, made by Khronos group).

2 — Run through starter tutorials.

There is a tutorial series “Introduction to Shaders (Lighting)” on the pyopengl website that gives good practice. I didn’t understand everything at first but was able to start understanding concepts after forcing myself through a few tutorials. My process was to code up 2–3 tutorials without trying too hard to understand what I was doing. Then go back the next day and try to understand every line of code by typing out summaries at the the top of each script.

3 — Guidelines for these tutorials

The tutorials don’t work well with python 3 (you can’t install OpenGLContext). So you need to setup an environment with python 2 and then install opengl stuff in that environment:

The following are my takeaways from each tutorial. Keep in mind that these are not intended to substitute for the tutorials but rather fill in information I thought was missing or needed clarification; they are intended to be done alongside the original tutorials.

Tutorial 1

The point of this tutorial is to get started. You need two shaders, a vertex shader and a fragment shader. The vertex shaders processes each point/vertex that you pass in and returns position values for that point. The fragment shader returns colors for all the pixels that are bounded by 3 vertices. In otherwords it connects 3 vertices and returns colors for all the points in between them. With openGL we define vertices and then build all the objects we want to draw on screen using triangles. A vbo is an array that holds data that will go to your GPU. In openGL you define an array locally with numpy and then you bind it into the gpu and then you use pointers likeglVertexPointerfto point at the data in your vbo. When you call the draw method it looks for the vertex pointers you have created, reads the points in order, and draws them in batches of 3 as triangles on your screen. Here we draw a simple set of triangles and color them green.

https://github.com/yvan/nbsblogs/blob/master/pyopengl_tut/tutorial1.py

Tutorial 2

The point of this tutorial is to expand on the previous one by adding more colors to the fragment. To do this we will set a vertex color in our vertex shader and then pass this value into the fragment shader. The fragment shader automatically looks at the colors in each the vertices it gets for a fragment (each fragment should get 3 vertices because we draw triangles on the screen) and blends them for the fragment it is returning. This funky behavior is called interpolation and I think opengl uses Goraud Shading by default to do it. The varying type values allow use to set values in the vertex shader and then access the result of interpolation in the fragment shader. In other words anything you set as varying in the vertex shader will be interpolated by default in the fragment shader. I want to emphasize how weird this is because it confused me at first. The best way to think about the fragment shader seems to be to envision that is receives points from the vertex shader in batches of N (N=3, points of a triangle here) and then takes each point that is in between the batch of 3 (so every point inside the triangle) and runs it through your fragment shader on that point, determining which color blend of the original 3 it should use for that point. The fragment shader is called a lot so it is fairly important that it be efficient. The vertex shader is only called, say 9 times (since we have 3 fragments, 3 times per fragment) and so we’d rather put computation in the vertex shader and let opengl work its interpolation magic. If successful it should look like this:

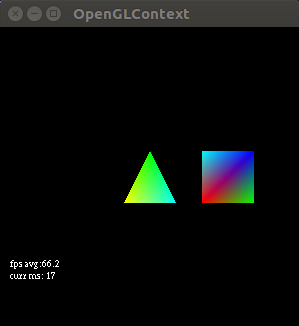
https://github.com/yvan/nbsblogs/blob/master/pyopengl_tut/tutorial2.py

Tutorial 3

The point of this tutorial is to introduce uniform values. Like varying value it can be used to share information between the vertex and fragment shaders but uniform values don’t get interpolated. Uniform values do not change for a whole rendering pass; they may change on the next rendering pass. So in this tutorial we setup a uniform fog value and based on the distance you are viewing the triangles from the fog gets thicker (further away) or thinner (if you are very close). Importantly I have changed my fog to be black, instead of white like the original tutorial, to match my black openglcontext background.

https://github.com/yvan/nbsblogs/blob/master/pyopengl_tut/tutorial3.py

Tutorial 4

The point of this tutorial is to introduce attribute values. Here we learn that the glVertexPointerandglColorPointerare legacy opengl. Instead in modern opengl we useglVertexAttribPointerwhich can point to arbitrary data. In this tutorial we create an animation where every frame of the animation calls a function named OnTimerFraction. Inside this function we set a fraction (called the tween) that tells us the proportion in which to combine 2 points. In our shader we then use the mix function to find a point between the point and a secondary position. If you do it correctly it will look like this, finding some intermediary point for every frame of the animation between two stated positions:

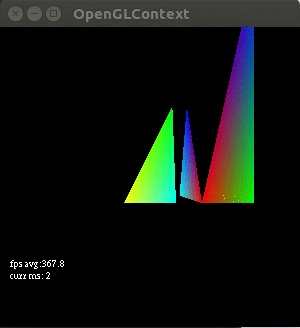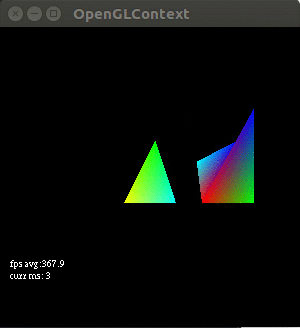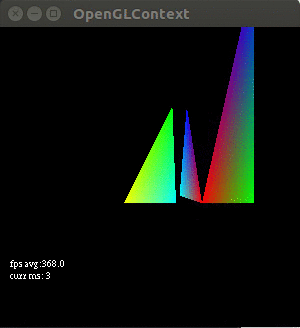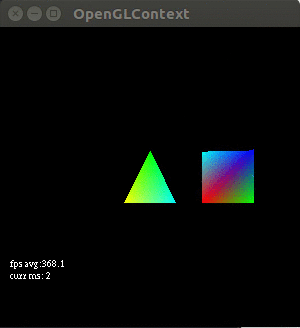
https://github.com/yvan/nbsblogs/blob/master/pyopengl_tut/tutorial4.py

Tutorial 5

The point of this tutorial is start examining lighting (an entire graphics subfield in itself). In this tutorial we are going to create an object in space and then apply ambient and diffuse lighting to the object. Ambient lighting is light that the object emits if there are no other lights, this is like the base color or shape from your current viewpoint. Diffuse lighting is light that the object emits evenly in all directions from the point where a light ray hits it, things that have a high diffuse reflectance would be objects with a matte finish.

The ambient light is just a multiplication of two constant values, the Light_ambient value (the amount of ambient light in our virtual environment) and the Material_ambient value (a value that represents the material’s sensitivity to reflect ambient light).

In this tutorial we also introduce the concept of phong shading (for the diffuse light). This method of shading takes the position of a light vector, and the normal for the fragment we are trying to shade and calculates the dot product, dot(normal_vector, light_vector). The result is used as a weight to multiply the diffuse light value by. The dot product calculates the component of the original light ray that lies along normal, in other words, how much light the normal/this vertex should reflect. We actually do all this in the vertex shader (using a Vertex_normal that we pass in for each vertex), add all these light values into the color (a varying value), then interpolate the results in the fragment shader.

https://github.com/yvan/nbsblogs/blob/master/pyopengl_tut/tutorial5.py

Tutorial 6

This tutorial introduces several new concepts. The first is indexed rendering, this is fairly simple, instead of defining points in order of rendering. We define a set of points; the order in which we use them is just a list of numbers (index into the set of points) that tells us which point to use. We use the Sphere function from scenegraph.basenodes to generate the vertices and the index into those vertices. The benefit of this is we can store only the information we need and avoid storing redundant vertices (when you get more complex structures with lots of repeated vertex use the performance is a lot better). We also use something called blinn-phong shading, a simplified version of phong shading, for specular light reflections. Blinn shading takes a half light vector, a vector that points out at an angle that is one half the angle between the light source and our viewpoint. The reason for doing this is because for specular light we need to take the dot product of the reflected light vector and the view vector. Often though the angle between our view and our reflected light is bigger than 90 degrees. This makes the phong caculation (dot product, cos(x>90)) difficult to work with (negative values). So blinn figured out that taking the dot product between the half light vector and the normal vector works and returns a viable weight (amount of reflection) for specular light. Imagine you are moving along a wireframe pixel by pixel calculating which light values each pixel should reflect. In tutorial 6 this is very much the case as our phong calculation is in the fragment shader, which means it’s run for every pixel in the fragment. Well if you have to take the dot product between the reflected specular light (changes for every pixel) and the angle of view (doesn’t change)this is going to change for every pixel. Every pixel reflects some different vector. The half light vector between your view (which doesn’t change) and the light source (whose vector doesn’t change) is a constant. So using the blinn model is actually cheaper computationally for specular lighting.

This photo demonstrates ambient + diffuse + specular lighting using blinn-phong shading very well:

https://github.com/yvan/nbsblogs/blob/master/pyopengl_tut/tutorial6.py

How to think about light rays, reflections, normals, and our viewpoint.

V is the view vector that represents our viewpoint. N is the normal, the vector that is predefined and that points out of this fragment. L is the ray from the light source. R is the specular reflected ray from the light source. H is the ‘half light vector’ for calculating blinn shading (vector between V and L). Something you will notice about all these vectors is that: 1-they point outward, 2-they all originate at a single point, 3-the vectors have the same length. All the vectors point outwards to make calculating dot products easier (counter intuitive for V and L). All the vectors originate at a single point or vertex, that is how our data is defined and it makes it possible to calculate light in the vertex shader. We call normalize on the vectors before doing dot products, this gets our vectors in the same length, we do this because we only care about the directions of the light and viewpoint for calculating the weightings in these exercises, not the magnitude.

Tutorial 7

The purpose of this tutorial is to do a little code cleanup and show an example of what using multiple lights looks like. One thing we did was move material properties (i.e. ambient material, diffuse, specular reflectance vales) into a structure instead of just setting them as global uniform values. We also setup 3 lights; for each light we provide ambient, diffuse, specular, and position vectors each with size 4. We show how to store these lights and their component vectors in a special array and populate this array with glUniform4fv. If you do tutorial 7 correctly you should get:

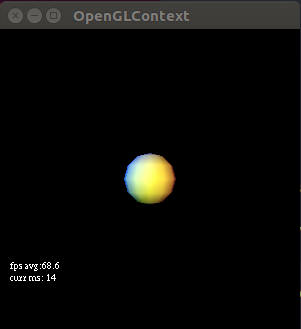
https://github.com/yvan/nbsblogs/blob/master/pyopengl_tut/tutorial7.py

In the guide the code says to take any dot products of the normal, reflected light vectors that are greater than -0.05 and only calculate the specular component for those. I’m not sure what this does because if we remove the if statement the result is quite similar. Also taking the max of 0 and anything should always be 0 at the lowest so why make the threshold -0.05? I’m going to investigate

Investigation as to why the cutoff produces a smooth effect

At first I thought the code for making specular reflection in tutorials 6,7 was simple but I realize there is some level of subtlety to it. We are going to run the tutorial 6 phong_weightCalc function:

If we leave the threshold at -0.05 we get a result:

if (n_dot_pos > -0.05)

If we change the threshold to a hard 0.0 in the if statement we get this:

if (n_dot_pos > -0.05)
--->
if (n_dot_pos > 0.0)

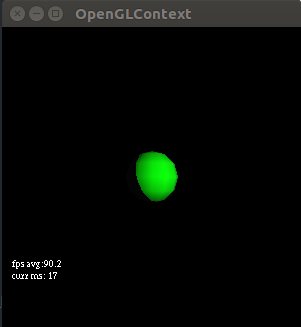
It is a weird cut off sphere. The cutoff actually doesn’t make sense. In theory even the parts that are not hit by the specular light should be illuminated via ambient light, we should still see something on the dark side? Ok so I just tested increasing the ambient light and a faint outline does show up on the dark side (Figure 3):

glUniform4f( self.Light_ambient_loc, .1,.1,.1, 1.0 )
-->
glUniform4f( self.Light_ambient_loc, 1.0,1.0,1.0, 1.0 )

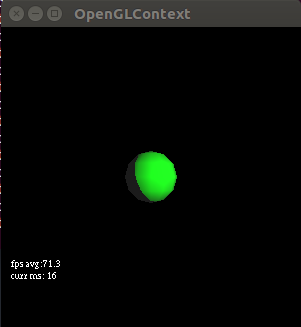
I will leave the ambient light like this as it makes things more visible/comparable. The thing that is a bit weird is that this if statement always fires when the threshold is set at -0.05. I know because if we remove the if statement we get an output like Figure 1 again; so it is like the if statement does not matter. This make sense, we maxed n_dot_pos with 0 meaning any negative result of the dot product would default to 0. Lets see what specular light is reflected for just the dot products that are 0.0:

if (n_dot_pos == 0.0)

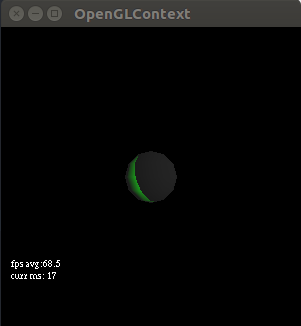
Ok so even when our light source is perfectly perpendicular to the normals it still produces a small band of green light for the specular reflection. Let’s max the dot product with -0.05 and set the threshold for n_dot_pos back to > -0.05 and also try ≥ -0.05 to see if this makes a difference:

float n_dot_pos = max(-0.05, dot(frag_normal, light_pos));

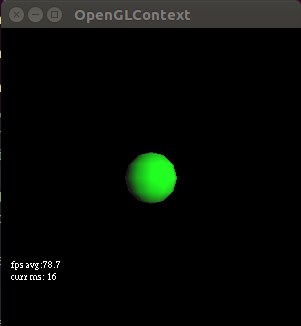
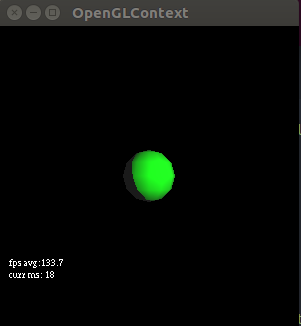
This makes sense all the dot products that are very negative get set to -0.05 and are included in the specular lighting so we get a bigger green reflection on the sphere on the left. It is bigger and still doesn’t include all the surface (we still see some ambient peeking out from behind) because when we take the dot product of the half_light vector and our view vector (after checking the n_dot_pos) some results will still be 0, showing only ambient light and no specular light. In the right image all these negative values get set to -0.05 and aren’t included by the > comparator and thus we get a more brutal cutoff. In conclusion: if you want a smoother cutoff for your specular light you need to max by and make sure that value is included in your comparator. So the original works but only because 0.0 is always > -0.05. You might as well use this function (which i’ve added to my tutorial 7 code):

General Notes:

I have added annotations for the first 7 tutorials as you can see there are many more in the opengl tutorial page. Feel free to do them!

You may notice a lot of calls to the normalize function in our opengl shader code; this just gets our vectors converted to unit vectors pointing in the same direction. We just want the directions of a lot of vectors and don’t care about magnitude.

It’s really easy to misspell something like glVertexAttribArray and then your program will run but won’t render and may fail silently. I’m not sure if this is a result of the OpenGLContextbut it happens. To prevent this be careful when typing out the names of things.

Dot products are |A| * |B| * cos(ø) where ø is the angle between vectors A and B; dot products are scalar. The dot product is always zero when two vectors are at a 90º angle to each other because cos(90º) = 0. This is a great explanation on mathisfun.

Conclusion

Shaders are really cool. If you’re interested in blogs like the one I just wrote you can sign up for my newsletter Generation Machine where I tend to keep readers up to date on the stuff I write. You can also checkout my previous post where I used pygame to generate a dataset of 3D cubes. Also I want to leave a final note here. It could be something I’ve said above is wrong, as always; enjoy your day.

Some other resources:

https://www.labri.fr/perso/nrougier/python-opengl/#python-opengl-for-scientific-visualization (a really cool book by nicolas rougier on python + opengl, this book seems very high quality and i’ve been using it as a reference)

https://thebookofshaders.com + https://www.shadertoy.com (pretty sure you can use anything with openGL 2+ (in the shadertoy app), webGL online, here).

https://webglfundamentals.org/webgl/lessons/webgl-shaders-and-glsl.html (webgl fundamentals)

https://vulkan-tutorial.com/Drawing_a_triangle/Graphics_pipeline_basics/Shader_modules(guide to using Vulkan)

https://github.com/realitix/vulkan (python vulkan bindings, so you can use Vulkan in python)

https://github.com/mackst/vulkan-tutorial (python vulkan tutorial)

https://www.opengl.org/archives/resources/features/KilgardTechniques/oglpitfall/ (common pitfalls using opengl)